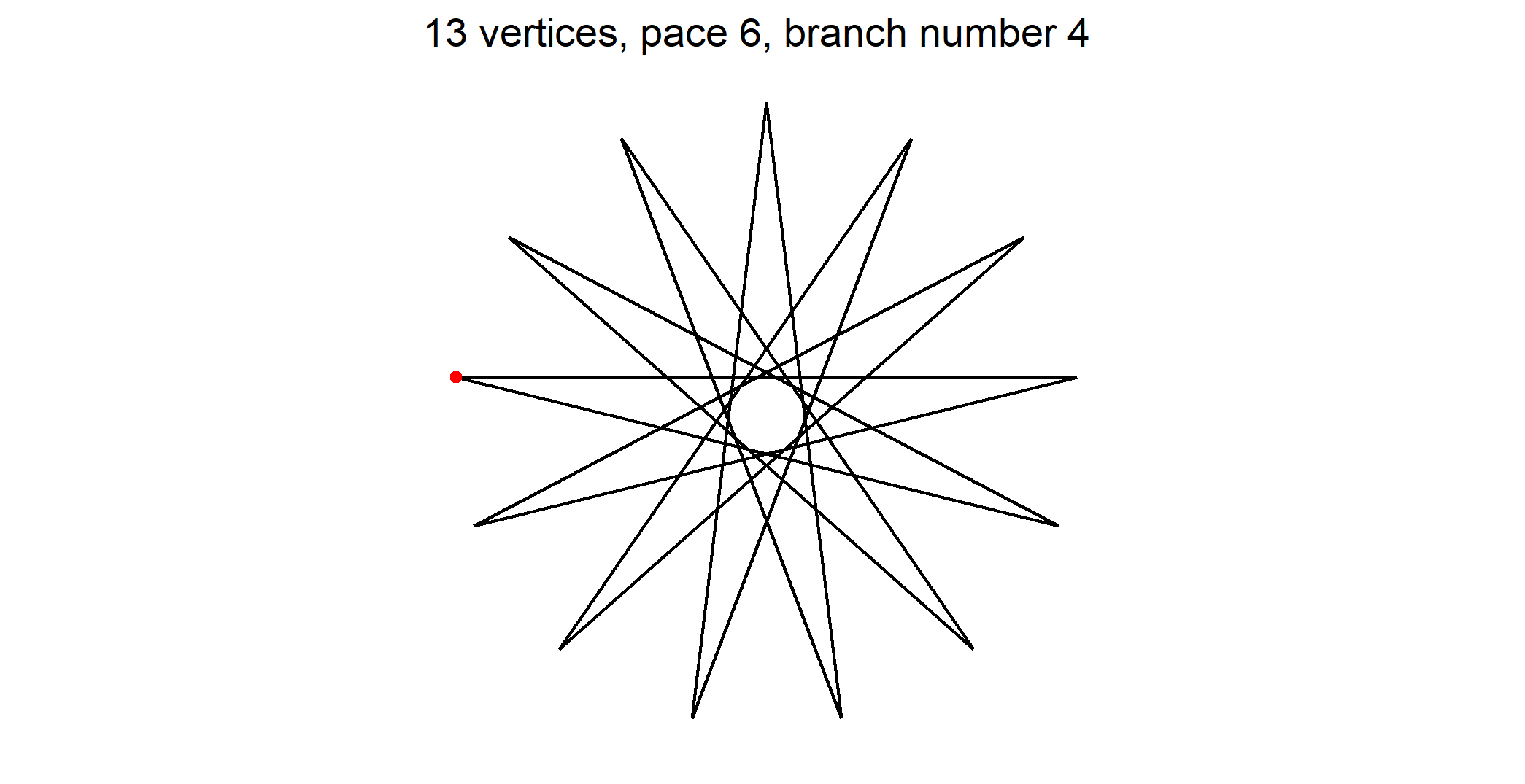
R - n-gons
23 Sep 2019
Problem statement
My interest is about polygons where the number of vertices is a prime number higher or equal to 5. When considering only star polygons I wish to have a synthetic formula to compute the included circles radiuses without even drawing any figure.
Some mathematics first
Number of polygons
For a given prime number p the number of related p-gons is given by the formula
Ω(p)=1 + (p − 1)/2
Note that all those polygons are different. Among them only the first one is a regular polygon. All others are star polygons defined by the fact that their drawing pictures implies intersections between segments.
Drawing polygons
From the same set of p starting points on the unit circle we can draw Ω(p) p-gons and each of them is unique. An easy way to draw them is to set a rule that allows to skip k points on each segment.
The regular polygon is of pace 1 and ties vertex #1 to vertex #2 and then vertex #2 to vertex #3 and so on.
The first star polygon is of pace 2 and ties vertex #1 to vertex #3 and then vertex #3 to vertex #5 and so on.
Each segment ties two and only two points of the unit circle. The pace has following properties
- 1 ≤ ρ ≤ Ω(p)
- When pace ρ = 1 the resulting draw is the regular polygon.
- When pace ρ > 1 the resulting draw is a star polygon.
Let’s see an example for a the case where p = 13. Here Ω = 6. So there are one regular pentagon and five star pentagons. Here they are
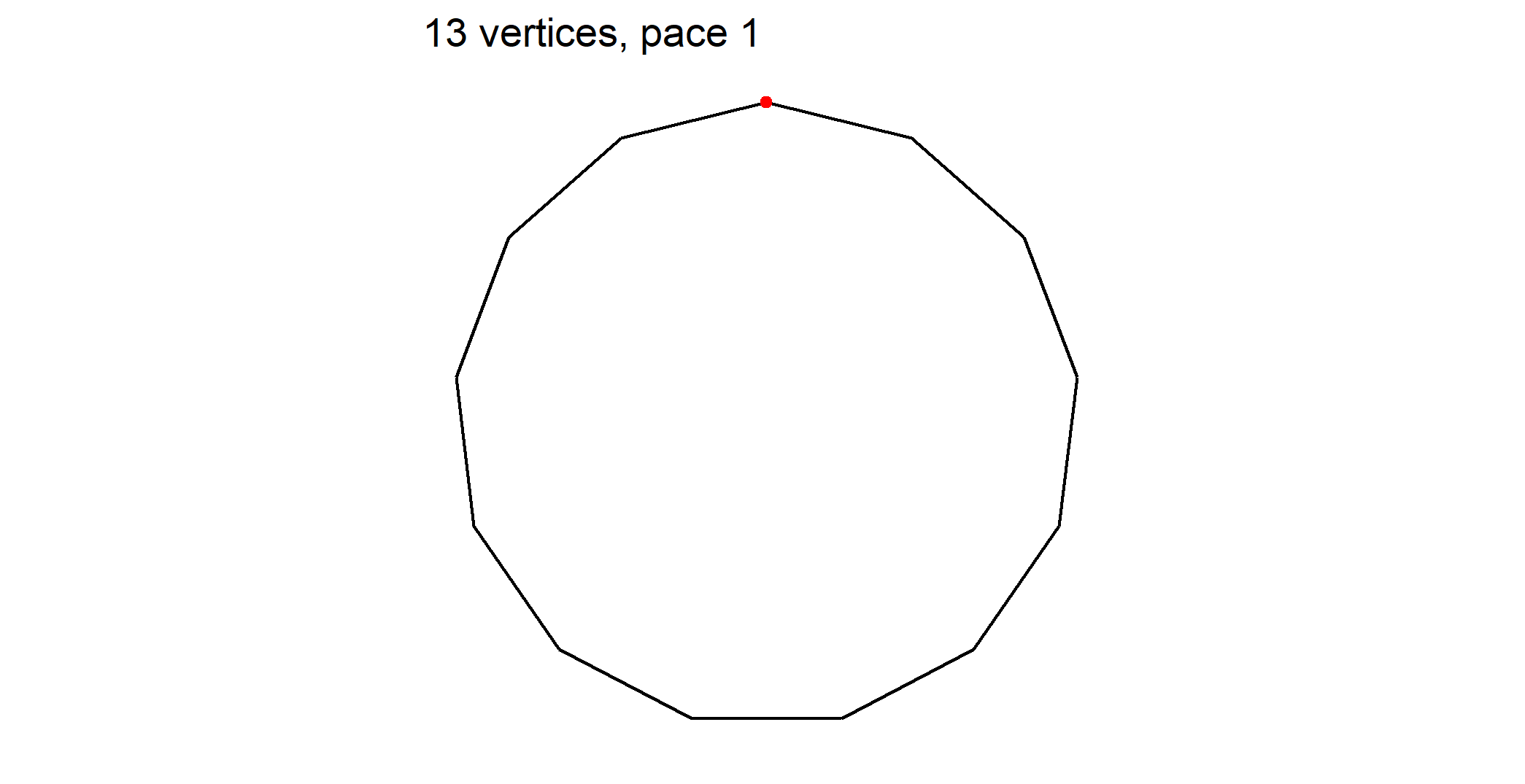
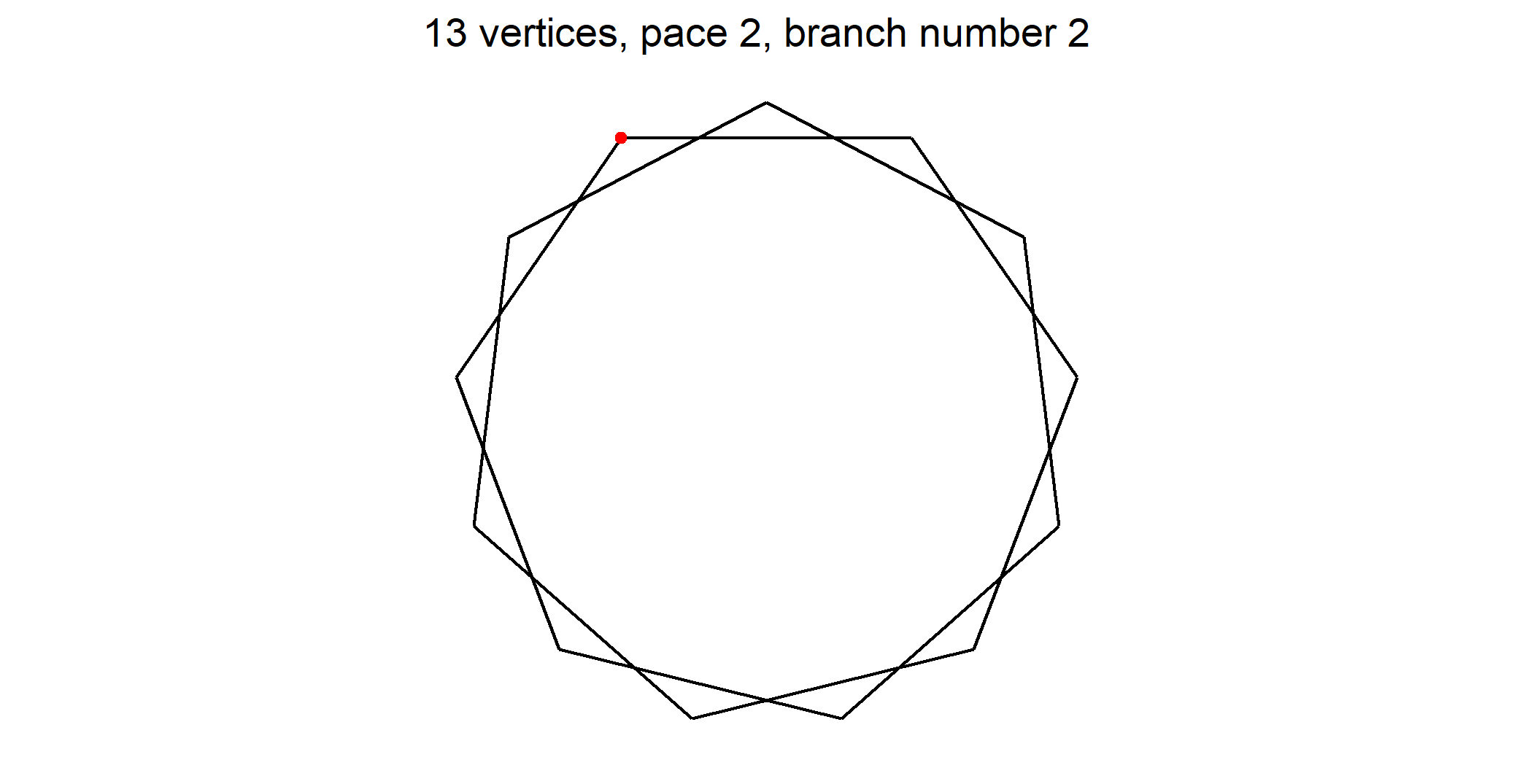
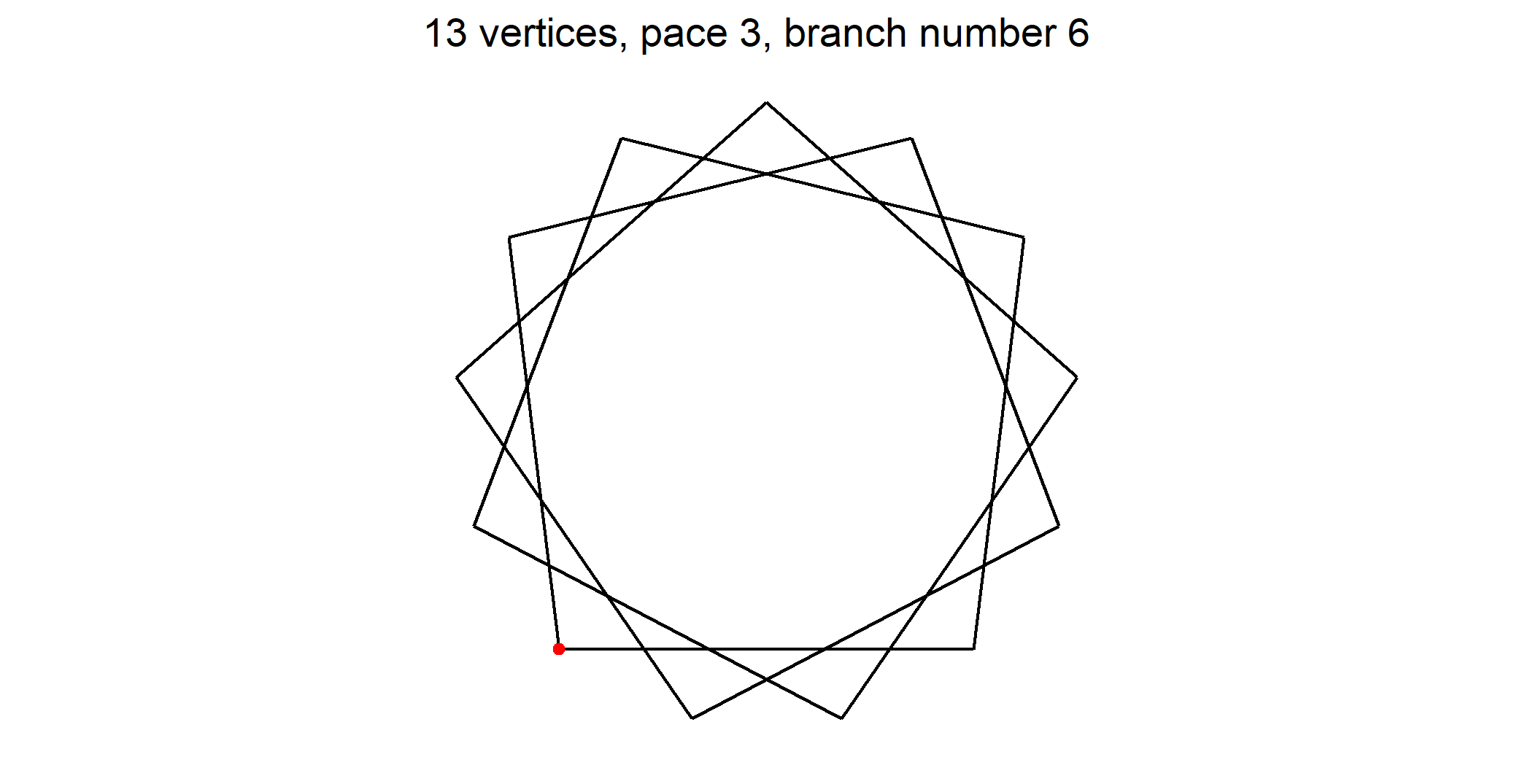
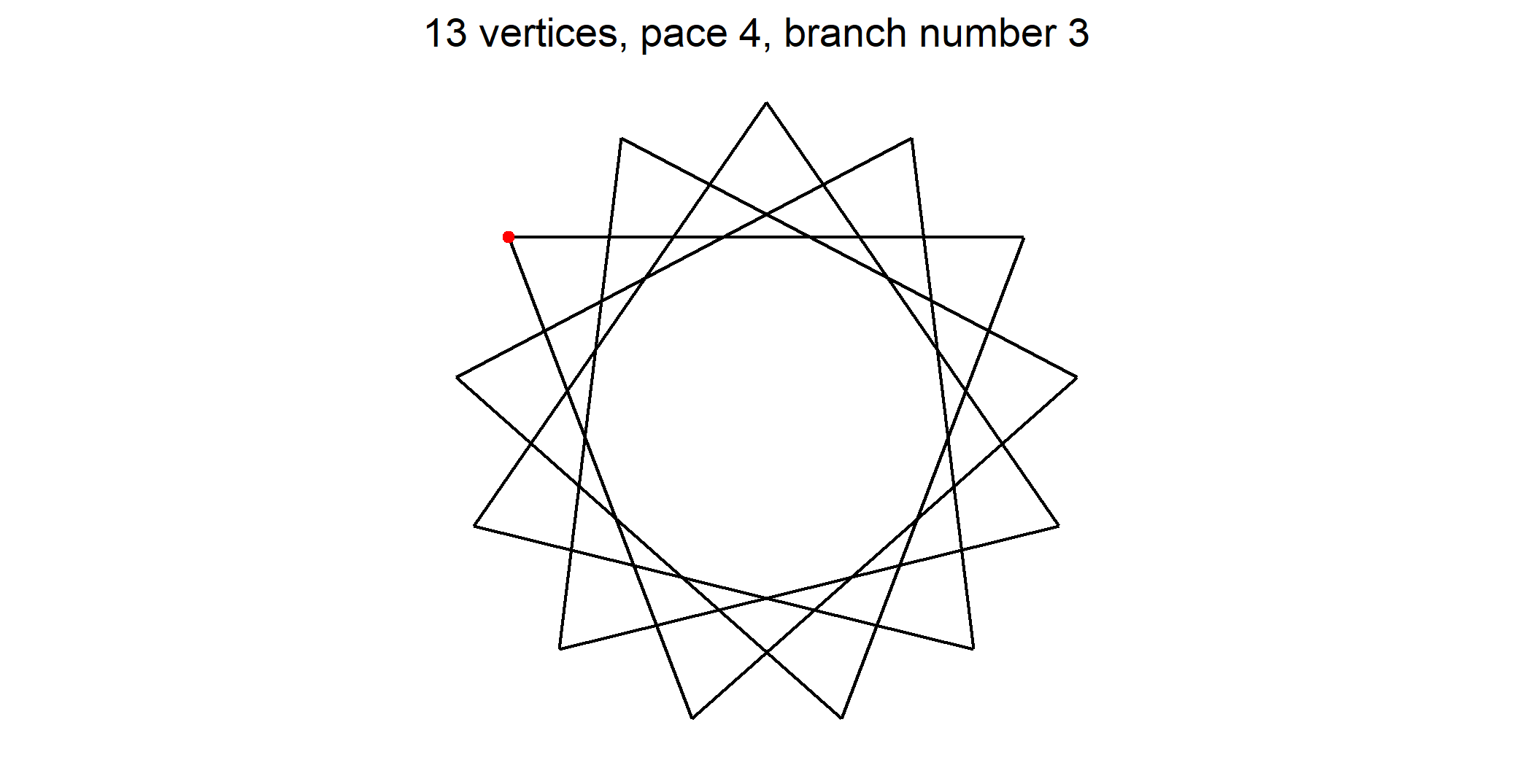
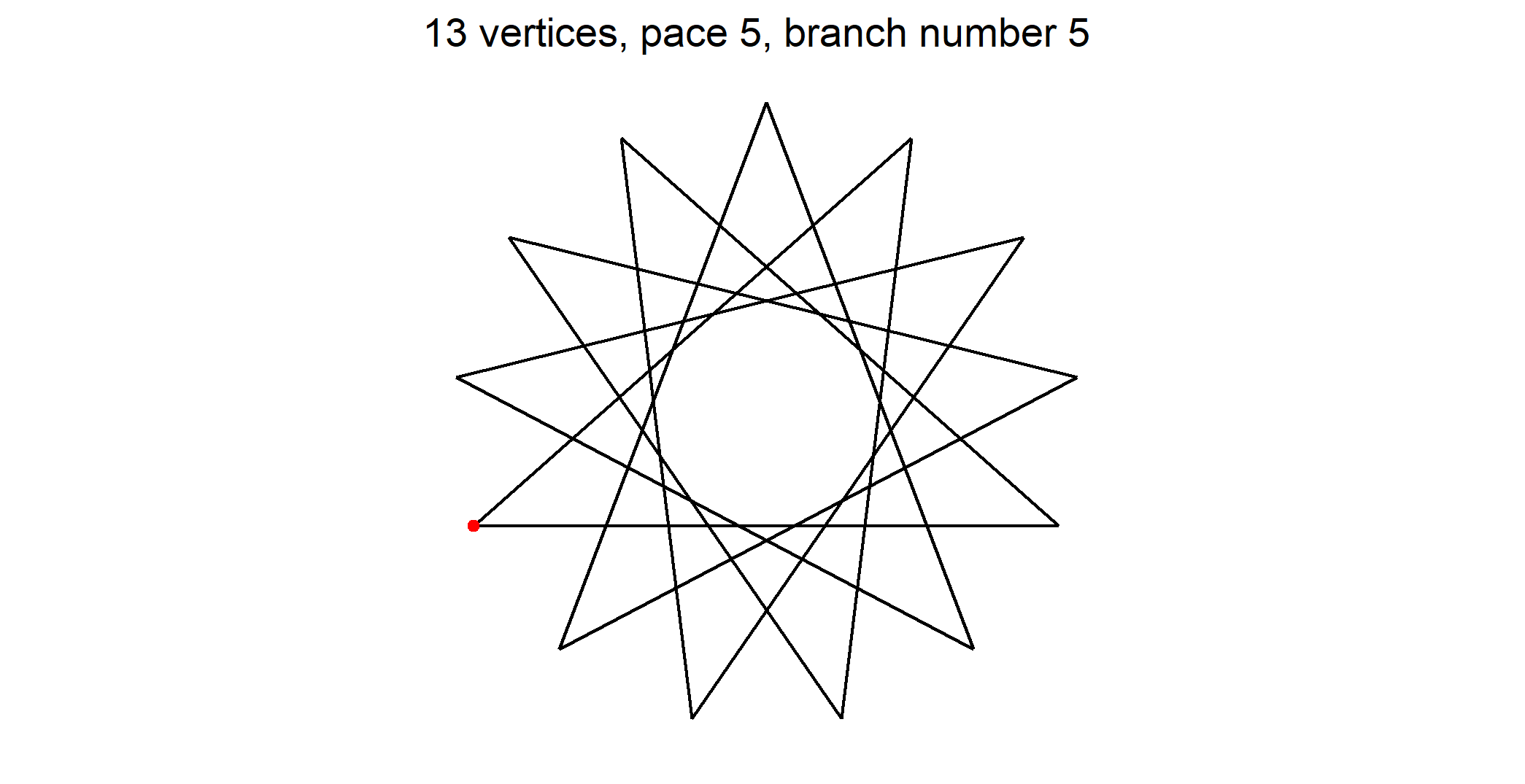

Red dot on a regular polygon shows point numbered 1 that is the starting point we index other points from. As it exists a vertical axis symmetry you may number clockwise or counter clockwise. On figures I took the choice to number counter clockwise (mathematical way).
Two more complex examples. First about 17-gons second about 89-gons.
A special suite
Its definition
Let’s consider following suite named ν(ρ p) where p is the chosen prime and ρ the pace of the star polygon. Suite ν takes values in ℕ for each parameter and gives back values in ℕ.
- The length λ of the suite ν(ρ p) is λ(p)=⌊(p − 1)/2⌋−1
- ν(2 p)=2 the first term is the pace of the first star polygon i.e. 2
- ν(3 p)=(p − 1)/2
- ν(n + 2 p)=ν(n p)+1 when n is even
- ν(n + 2 p)=ν(n p)−1 when n is odd
- Last term η is η = (ν(2 p)+ν(3 p))/2 = (2 + (p − 1)/2)/2 = (p + 3)/4
Some instances of ν
| prime | ν | λ |
|---|---|---|
| 5 | 2 | 1 |
| 7 | 2 3 | 2 |
| 11 | 2 5 3 4 | 4 |
| 13 | 2 6 3 5 4 | 5 |
| 17 | 2 8 3 7 4 6 5 | 7 |
| 19 | 2 9 3 8 4 7 5 6 | 8 |
| 23 | 2 11 3 10 4 9 5 8 6 7 | 10 |
| 29 | 2 14 3 13 4 12 5 11 6 10 7 9 8 | 13 |
| 31 | 2 15 3 14 4 13 5 12 6 11 7 10 8 9 | 14 |
| 37 | 2 18 3 17 4 16 5 15 6 14 7 13 8 12 9 11 10 | 17 |
| 41 | 2 20 3 19 4 18 5 17 6 16 7 15 8 14 9 13 10 12 11 | 19 |
| 43 | 2 21 3 20 4 19 5 18 6 17 7 16 8 15 9 14 10 13 11 12 | 20 |
| 47 | 2 23 3 22 4 21 5 20 6 19 7 18 8 17 9 16 10 15 11 14 12 13 | 22 |
| 51 | 2 26 3 25 4 24 5 23 6 22 7 21 8 20 9 19 10 18 11 17 12 16 13 15 14 | 25 |
The suite seems to oscillate from highest span to lowest span until span vanishes (δ = ν(n p)−ν(n + 1 p)=1). To see it focus on the red dots of star polygons in movies above.
Solution of the stated problem
Let’s name ϕ the function that computes the included circles radiuses given the pace ρ as parameter
ϕ(ρ) = |sin(pi/2 + (ν(ρ, p) - 1) * 2 * pi /p)|
Some instances of ϕ
| prime | ν | ϕ |
|---|---|---|
| 5 | 2 | 0.309016994374948 |
| 7 | 2 3 | 0.623489801858734 0.222520933956314 |
| 11 | 2 5 3 4 | 0.841253532831181 0.654860733945285 0.415415013001886 0.142314838273285 |
| 13 | 2 6 3 5 4 | 0.88545602565321 0.748510748171101 0.568064746731156 0.354604887042536 0.120536680255323 |
| 17 | 2 8 3 7 4 6 5 | 0.932472229404356 0.850217135729614 0.739008917220659 0.602634636379256 0.445738355776538 0.273662990072083 0.0922683594633018 |
| 19 | 2 9 3 8 4 7 5 6 | 0.945817241700635 0.879473751206489 0.789140509396394 0.677281571625741 0.546948158122427 0.40169542465297 0.245485487140799 0.0825793454723324 |
| 23 | 2 11 3 10 4 9 5 8 6 7 | 0.962917287347799 0.917211301505453 0.854419404546489 0.77571129070442 0.682553143218654 0.576680322114867 0.460065037731152 0.334879612170986 0.203456013052634 0.068242413364671 |
| 29 | 2 14 3 13 4 12 5 11 6 10 7 9 8 | 0.976620555710087 0.947653171182802 0.907575419670957 0.856857176167589 0.796093065705644 0.725995491923131 0.647386284781828 0.561187065362382 0.46840844069979 0.370138155339914 0.267528338529221 0.161781996552764 0.0541389085854179 |
| 31 | 2 15 3 14 4 13 5 12 6 11 7 10 8 9 | 0.979529941252494 0.954139256400049 0.918957811620231 0.874346616144582 0.820763441207276 0.758758122692791 0.688966919075687 0.612105982547662 0.528964010326963 0.440394151557634 0.347305252844821 0.25065253225872 0.151427777504577 0.0506491688387124 |
| 37 | 2 18 3 17 4 16 5 15 6 14 7 13 8 12 9 11 10 | 0.985615910347708 0.967732946933499 0.942877445461084 0.911228490388136 0.873014113161188 0.828509649243842 0.77803575431844 0.721956093954524 0.660674723390081 0.594633176304287 0.524307283557232 0.450203744817673 0.372856477780309 0.29282277127655 0.210679269995726 0.127017819746879 0.0424412031961485 |
| 41 | 2 20 3 19 4 18 5 17 6 16 7 15 8 14 9 13 10 12 11 | 0.988280423780349 0.973695423877779 0.953396392054931 0.927502451102095 0.896165556961056 0.859569606987201 0.817929360766718 0.771489179821943 0.720521593600787 0.665325700165565 0.606225410966638 0.543567550001221 0.477719818512263 0.40906863717134 0.338016878408503 0.264981502196661 0.190391109164668 0.1146834253984 0.0383027336900356 |
| 43 | 2 21 3 20 4 19 5 18 6 17 7 16 8 15 9 14 10 13 11 12 | 0.98934336807511 0.976075877555927 0.957600599908406 0.934016108732548 0.905448237493147 0.872049408143808 0.833997817889878 0.791496488429254 0.744772182743782 0.694074195220634 0.639673021558891 0.581858915557953 0.52094034048793 0.457242323304638 0.391104720490156 0.322880404771446 0.252933382391681 0.181636850979436 0.109371208377875 0.0365220230576584] |
| 47 | 2 23 3 22 4 21 5 20 6 19 7 18 8 17 9 16 10 15 11 14 12 13 | 0.98934336807511 0.976075877555927 0.957600599908406 0.934016108732548 0.905448237493147 0.872049408143808 0.833997817889878 0.791496488429254 0.744772182743782 0.694074195220634 0.639673021558891 0.581858915557953 0.52094034048793 0.457242323304638 0.391104720490156 0.322880404771446 0.252933382391681 0.181636850979436 0.109371208377875 0.0365220230576584 |
| 51 | 2 26 3 25 4 24 5 23 6 22 7 21 8 20 9 19 10 18 11 17 12 16 13 15 14 | 0.99107748815478 0.979961705036587 0.964469175054377 0.944669091607919 0.920649886676429 0.892518835859881 0.860401579260139 0.82444156034176 0.784799385278661 0.741652105647957 0.695192427674642 0.645627851558802 0.593179744729355 0.538082353163373 0.480581755186684 0.420934762428335 0.359407772837513 0.296275580885634 0.231820150267529 0.16632935458313 0.100095691624099 0.0334149770076742] [0.992981096013517 0.984230577947597 0.972022914080411 0.956400984276522 0.937419661134121 0.915145617243018 0.889657090994747 0.861043611767355 0.829405685450202 0.794854441413353 0.75751124216162 0.717507257044331 0.674983001518211 0.630087843581711 0.582979479114472 0.533823377964791 0.482792202730745 0.430065202276521 0.375827582114238 0.320269853862838 0.263587166069068 0.205978618741098 0.147646564002482 0.0887958953229347 0.0296333278225597 |
Note as expected included circles radiuses are in descending order.